




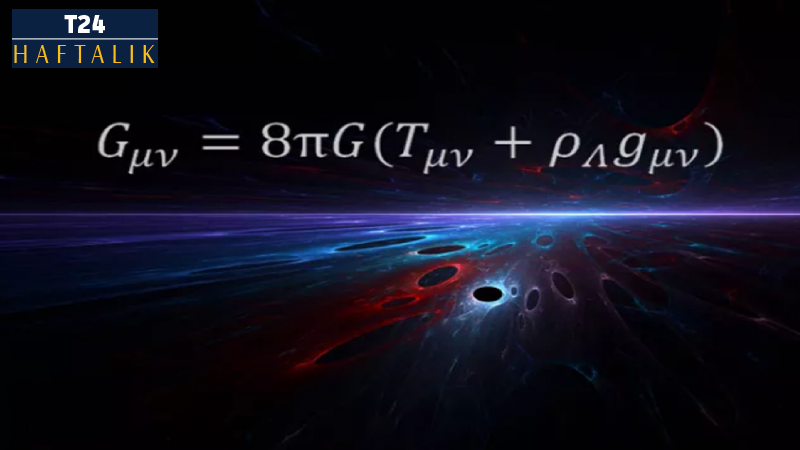
Bizim gerçekliğimizde matematik denklemler doğayı ve evreni yöneten kuralları ifade ederler.
Matematik bu anlamda doğanın dilidir. Her kültürden, her bilim alanından tüm bilim insanları bu ortak dili kulanırlar.
İkinci bir dili öğrenmek gibi, matematik öğrenmek ve anlamak da yıllarca süren bir eğitimi gerektiriyor. Eğer bu dili bilmiyorsanız, matematik denklemleri anlamak için bazan kitaplar dolusu açıklamalar bile yeterli olmayabilir.
Bir matematik denklem, kısa bir tanımla, farklı niceliklerin eşitliğini gösteren bir bağıntıdır, y= kx gibi. Ve bu eşitliğin gerisinde ciddi bir bilgi desteği ve şaşırtıcı bir güç bulunur.
Ünlü İngiliz fizikçi Paul Dirac, "Fizik yasaları, matematiksel güzellik barındırmalı ve basit olmalıdır" derken kitaplar dolusu bilginin bir satırla ifade edilebilen bir denklemin uyumunu ve estetik yanını dile getirir.
BBC Earth, 2016 yılında matematikçilerden ve fizikçilerden, listelediği 12 denklem içinden "en güzel"ini seçmelerini istedi.
Sonuçlar oldukça çarpıcı. Bu oylamaya göre en güzel denklem tartışmasız "Dirac Denklemi".
"Fizik yasaları, matematiksel güzellik ve basitliğe sahip olmalıdır" diyen Dirac, en güzel denklemin de yaratıcısı olarak açık ara birinci.
Aşağıda sonuçları görüyorsunuz:

Dirac denklemi "en güzel" olan; peki, onlar içinde "en güçlü" olan hangisi?
Muhtemelen hepsi.
Ancak bazı denklemler diğerlerinden çok daha geniş etkiye ve güce sahiptirler.
Birçok bilim insanı, özellikle fizikçiler, en güçlü denklem olarak iki denklem üzerinde hemfikir: Einstein patentli olan bu denklemler, kütle-enerji ve uzay-kütle eşdeğerliği üzerinden tanımlı.
Einstein, bir anlamda evreni bu iki güçlü denklemle özetliyor.
1905 yılında yayınladığı kütle ve enerji eşdeğerliğinin ifadesi olan E=mc2 denklemi basit, kolay anlaşılır ve çok güçlü bir denklem olarak kabul görmekte.
Bu denklemde iki farklı parametre, kütle ve enerji, bir şekilde eşitlenmiş.
Yıldızlardaki füzyon enerjisinin ve geçmişte acıyla deneyimlediğimiz atom enerjisinin kaynağı olan kütlenin enerjiye dönüşmesi olgusunu bu denklemler aracılığıyla anlıyoruz.
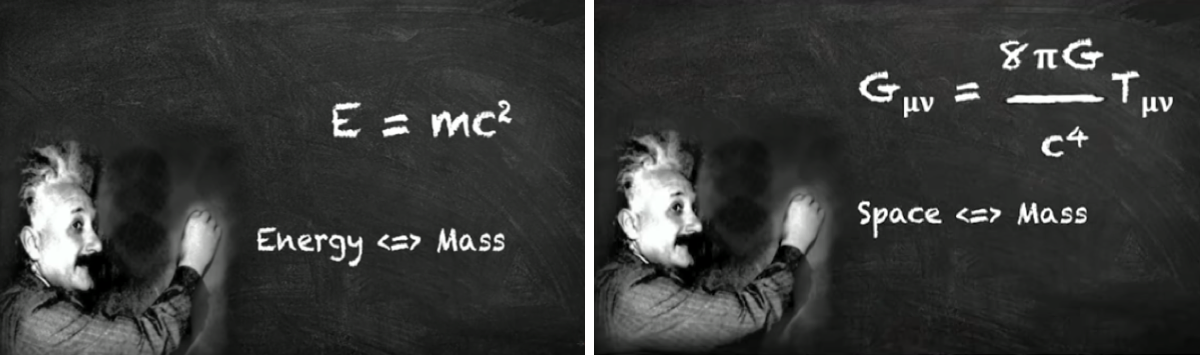
Ayrıca enerjiden parçacık oluşacağını da bu denklem bize söylüyor: Fizikte çift oluşum gibi, ya da Büyük Patlama ile fışkıran enerjinin maddeye dönüşümü gibi.
İkinci denklem çok daha güçlü, ancak daha karmaşıktır; ilk denklem kadar çok bilinir olmasa da evreni anlamada çok daha fazlasını sunuyor.
Einstein bu kez kütlesel çekimi ve uzay-zamanın eğrilmesini tanımlamaktadır. Kısaca söylemek gerekirse, esnek uzay-zaman dokusunda ağır bir kütlenin nasıl eğrilik yarattığını ve kütlenin uzay-zamanda nasıl hareket ettiğini söylüyor.
Aynı bizim üzerinde durduğumuz platforma yaptığımız baskı gibi (eğer bastığımız yer esnek bir malzemeden yapılmış ise eğrilip çukurlaşacaktır), esnek uzay-zaman dokusunun üzerine konulan kütleli bir cisim uzay-zamanı bükecek ve çukurlaştıracaktır.
Denklemde, eşitliğin bir tarafı uzay zamanın nasıl eğrildiğini, diğer tarafı ise kütlenin nasıl hareket ettiğini ifade etmektedir.
Fizikçi John Wheeler'in tanımıyla: "Uzay-zaman, maddeye nasıl hareket edeceğini söylüyor; madde de uzay-zamana nasıl eğrileceğini."
Dünya etrafında dönen Ay'ı göz önüne alalım. Dünya, kütlesi nedeniyle uzay zamanda bir eğrilik yaratıyor ve Ay olabildiğince düz bir yol almaya çalışırken Dünya'nın uzay-zamanda oluşturduğu eğrilik etkisiyle dönerek ilerliyor.
Bunun anlamı uzay-zaman ölçeğinde her şey döngüsel bir yol izlemek durumundadır; Işık bile!
Ancak bunu kanıtlamak çok da kolay değildir.
Einstein, Güneş tutulması sırasında ışığın davranışının izlenmesi için bir deney önerir.
Deney Mayıs 1919'da, yani tam 100 yıl önce İngiliz astronom Eddington tarafından gerçekleştirilir.
Bu olayda ışığın kütlesel çekimin etkisinde kalarak büküldüğü görülür ve Einstein öngörüsünde haklı çıkar.
Bu olaya kütleçekimsel mercek etkisi deniliyor.
Deneyin sonucu Einstein'a Hollandalı bilim insanı Lorentz tarafından bildirilir. Felsefe öğrencisi Ilse Schneider, tutulma sonuçları başka türlü olsaydı ne hissederdi diye sorduğunda, öngörülerinin doğrulanmadığı zamanlar söylediği ünlü sözü tekrarlar: “Sevgili Lord için üzülmem gerekirdi. Teori doğrudur ”
Bu büyük keşif, Einstein'a ebedi bir şöhret kazandırır.
 Lorentz'in Einstein'a deney ile ilgili bilgilendirme telgrafı
Lorentz'in Einstein'a deney ile ilgili bilgilendirme telgrafıEinstein'ın Görelilik Kuramlarını özetleyen bu iki ünlü denklem, daha önce çözülmemiş birçok soruya yanıt vermekle kalmadı; zamana, mekana ve yer çekimine bakış açımızı temelden değiştirdi. Gerçekliğin temel dokusu olan uzay-zamanın biçimlendirilebilir olduğunu anladık.
Dahası Büyük Patlama'dan karadeliklere, yıldızların enerjisinden nükleer güce ve akıllı telefonlarımıza kadar her sorunun yanıtını o denklemlerde bulabiliyoruz.
Akıl yaratıcıdır.
Evreni ve doğayı matematik denklemlere sığdırmak ise insan aklının en büyük yaratıcılığı.
Bu anlamda matematik hem güçlü hem de güzeldir, en güzeli ise onu anlayabilmek!
Kaynakça